Write the equation of the line

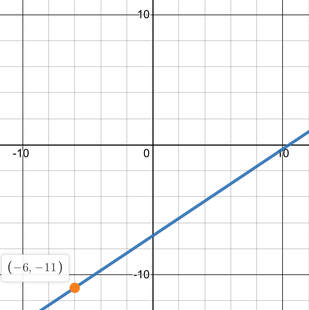
Write an equation that is parallel to 3x − 2y = 14 and passes through the point (-6, -11) in slope-intercept form.

---

Parallel lines have the same slope.  Get the given equation in slope-intercept form to find the slope.

Slope-intercept form is 
y = mx + b
m is the slope
b is the y-intercept

3x - 2y = 14  {given equation}
-2y = -3x + 14  {subtracted 3x from each side}
y = (2/3)x - 7  {divided each side by -2}
slope = 2/3

Use slope-intercept form, with the point and the slope, to get the equation of the line.  
Substitute (-6,-11) in for x and y, and 2/3 in for the slope.  Find the y-intercept, then substitute it back 
in, with the slope, into slope-intercept form.

(-6,-11), m = 2/3  {point and slope}
y = mx + b  {slope-intercept form}
-11 = (2/3)(-6) + b  {substituted point and slope into slope-intercept form}
-11 = -4 + b  {multiplied 2/3 by -6}
b = -7  {added 4 to each side}
y-intercept is -7

y = mx + b  {slope-intercept form}
y = (2/3)x - 7  {substituted point and slope into slope-intercept form}

Use the graphing calculator to check if the point does lie on the new line.

Ask the House