Verify the points lie on the same graph

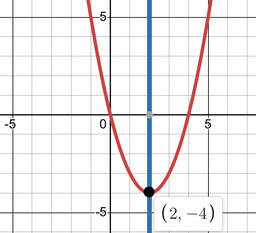
If the point (2 + d, y) is on the graph of the function f(x) = x(x – 4), then the point (2 – d, y) is also on the graph.  Use algebra to show that the claim is true.  What is the relationship between the line x = 2 and the graph of f(x)? Justify your reasoning.

---

If f(x) = x(x - 4)

When x = (2 + d)
f(x) = (2 + d)((2 + d - 4)  {substituted (2 + d) in for x, into f(x) = x(x - 4)}
f(x) = (2 + d)(-2 + d)  {combined like terms in parentheses}

When x = (2 - d)
f(x) = (2 - d)(2 - d - 4)  {substituted (2 - d), in for x, into f(x) = x(x - 4)}
f(x) = (2 - d)(-2 + d)  {combined like terms in parentheses}

With f(x) being the same, whether x is (2 + d) or (2 - d), this proves the claim is true.

The line x = 2 is the axis of symmetry of the parabola.  Using the graphing calculator, you can see x = 2 is the vertical line that passes through the vertex of the parabola f(x) = x(x - 4).

​Ask Algebra House
​