Find the probability

The two-way table shows the number of births, in thousands, in the United States for the years 2010 and 2011.

In February ~299 births in 2011 / total births in 2011 ~3,966

A baby born in 2011 is randomly selected.
What is the probability that the baby was born in February?

---

Probability of baby, who is born in 2011, being born in February.

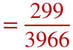
  {299 babies were born in February of 2011, and 3966 babies were born in 2011}

---

Also, if you meant 299,000 and 3,966,000 (since it says in thousands) the reduced answer would be the same.

Ask the House