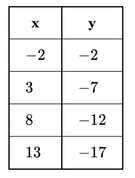
Find the equation of the linear function represented by the table

Find the equation of the linear function represented by the table below in slope-intercept form.

---

- To get the equation of a line, you need a point and a slope.
- Choose two points from the chart and find the slope of the line through those two points.

(-2,-2) and (3,-7)

-7 - (-2)
————— = slope  {change in y-coordinates over change in x-coordinates}
3 - (-2)

-5
—— = slope  {subtracted in numerator and denominator}
5

slope = -1

Take the slope, with one of the points, and substitute into slope-intercept form.

(-2,-2) , slope = -1

y = mx + b  {slope-intercept form}
​-2 = -1(-2) + b  {substituted -2 for x, -2 for y, and -1 for m}
-2 = 2 + b  {multiplied -1 by -2}
b = -4  {subtracted 2 from each side}
y-intercept = -4

Substitute the slope, -1, and the y-intercept, -4, back into slope-intercept form.

y = mx + b  {slope-intercept form}
y = -1x - 4  {substituted -1 for m, and -4 for b}

y = -x - 4 is the function represented by the table

Ask Algebra House