Identify the coefficient of x, in a quadratic equation {ACT}

In the equation x² + mx + n = 0, m and n are integers.  The only possible value for x is -3.  What is the value of m?
A.)  3
B.)  -3
C.)  6
D.)  -6
E.)  9

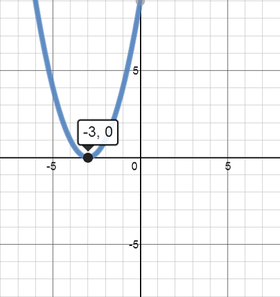
If the only possible value for x is -3, and it is a parabola, then the parabola would be touching the x-axis at -3, such as in the graph below:

If x = -3, and it is a parabola, then the solution would be -3 with a multiplicity of 2.
Work backwards from the solution:

x = -3 or x = -3   {set x = -3, twice, since the multiplicity of -3 is 2}
x + 3 = 0  or  x + 3 = 0   {added 3 to each side}
(x +3)(x + 3) = 0   {multiplied and set equal to 0}
x² + 6x + 9 = 0   {used foil method}

The value of m is 6.

C.)

- Algebra House