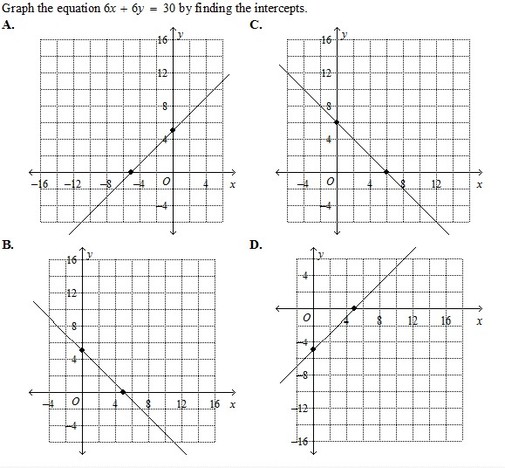
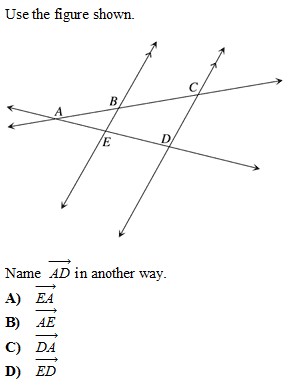
|
If a number is chosen at random from the set {-10, -5, 0, 5, 10}, what is the probability that it is a member of the solution set of both 3x - 2 < 10 and x + 2 > -8?
A.) 0 B.) 1/5 C.) 2/5 D.) 3/5 E.) 4/5 In the xy-plane, line l is perpendicular to the graph of the function f(x) = 5x - 2.
Line l could be the graph of which of the following functions? A.) g(x) = -5x B.) g(x) = (-1/5)x C.) g(x) = x - 2 D.) g(x) = (1/5)x E.) g(x) = 5x If x + y = a and x - y = b, then x =
A.) 1/2(a + b) B.) a + b C.) a - b D.) 1/2ab E.) 1/2(a - b) Which of the following is the equation of a straight line that has y-intercept 3 and is perpendicular to the line 4x - 2y = 6.
A.) 2y + 3x = - 3 B.) y + 3x = -2 C.) 2y - x = 6 D.) y - 2x = 4 E.) 2y + x = 6 |
Latest Videos
Archives
December 2023
ACT is a registered trademark of ACT, Inc. SAT is a registered trademark of the College Board. ACT and SAT are not affiliated with this site.
|