How to Graph a System of Inequalities

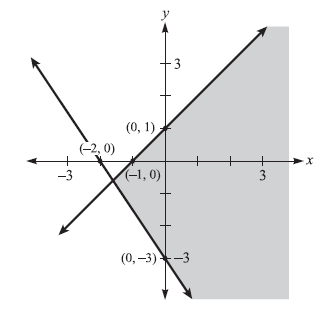
Which of the following inequalities is represented by the shaded region of the graph below ?

A.)  y ≤ x + 1  or  y ≥ x - 3
B.)  y ≥ x + 1  or  y ≤ x - 3
C.)  y ≤ x + 1  or  y ≥ (-3/2)x + 3
D,)  y ≤ x + 1  or  y ≤ (-3/2)x - 3
E.)  y ≤ x + 1  or  y ≥ (-3/2)x - 3

---

When graphing inequalities:

• ≤  and  ≥ signs indicate a solid boundary line, while <  and  >  signs indicate a dashed boundary line
• shading below the line indicates use of < or ≤ signs
• shading above the line indicates > or ≥ signs

First, locate the y-intercept of each line, while also determining the slope of each line.

One line
y-intercept is 1
slope is 1
Equation is y = x + 1
Also, the shading is below that line, and it is a solid line,
Therefore, the inequality is:
y ≤ x + 1   {boundary line is y = x + 1, using ≤ sign because of solid line, using ≤ sign because of shading below}

Other line
y-intercept is -3
slope is -3/2
Equation of boundary line is y = (-3/2)x - 3
Also, the shading is above that line, and it is a solid line.
Therefore, the inequality is:
​y ≥ (-3/2)x - 3   {boundary line is y = (-3/2)x - 3, using ≥ sign because of solid line, using ≥ sign because of shading above}

Put the two together, and you have:
E.)  y ≤ x + 1  or  y ≥ (-3/2)x - 3

Ask Algebra House
​