Finding the Area of a Triangle Using Coordinates

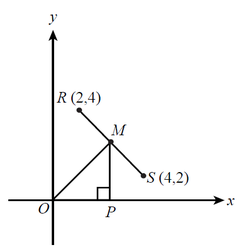
In the figure below, M is the midpoint of segment RS.  What is the area of  ∆MOP ?

A.)  4.5
B.)  4
C.)  3.5
D.)  3
E.)  2√2

If M is the midpoint of segment RS, then M has coordinates of (3,3).

Therefore,
- segment OP measures 3 units and
- segment MP measures 3 units

base x height
----------------- = area of a triangle
        2

∆MOP has a base of 3 and a height of 3

3 x 3
-------- = area of ∆MOP   {substituted base and height into area formula}
   2

= 9/2   {multiplied in numerator}
= 4.5   {divided}

Area of ∆MOP = 4.5

A.)  4.5 

Ask Algebra House