Find the missing side

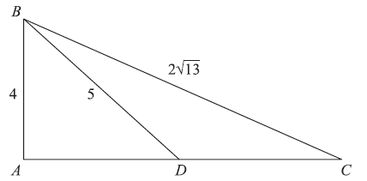
In the figure below, the lengths of right triangle BAC are shown.  Side BD bisects side AC.  What is the length of side CD ?

A.)  √3
B.)  2
C.)  3
D.)  2√5
​E.)  4

---

Use the Pythagorean Theorem in triangle BAC to find side AD which is congruent to side CD, since BD bisects AC.

Pythagorean Theorem
a² + b² = c²  {sum of the squares of the legs, a and b, is equal to the square of the hypotenuse}
4² + b² = 5²   {substituted legs and hypotenuse into Pythagorean Theorem}
16 + b² = 25   {evaluated exponents}
b² = 9   {subtracted 16 from each side}
b = 3  {took positive square root of each side}

C.)  3

Ask Algebra House