Prove the triangles are congruent

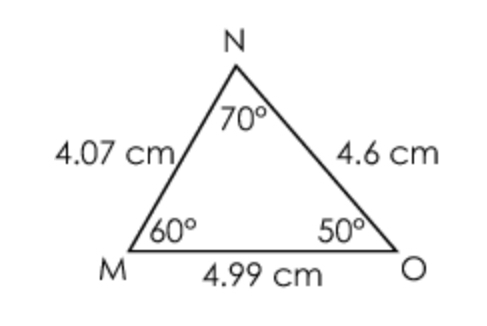
Triangle MNO is shown.

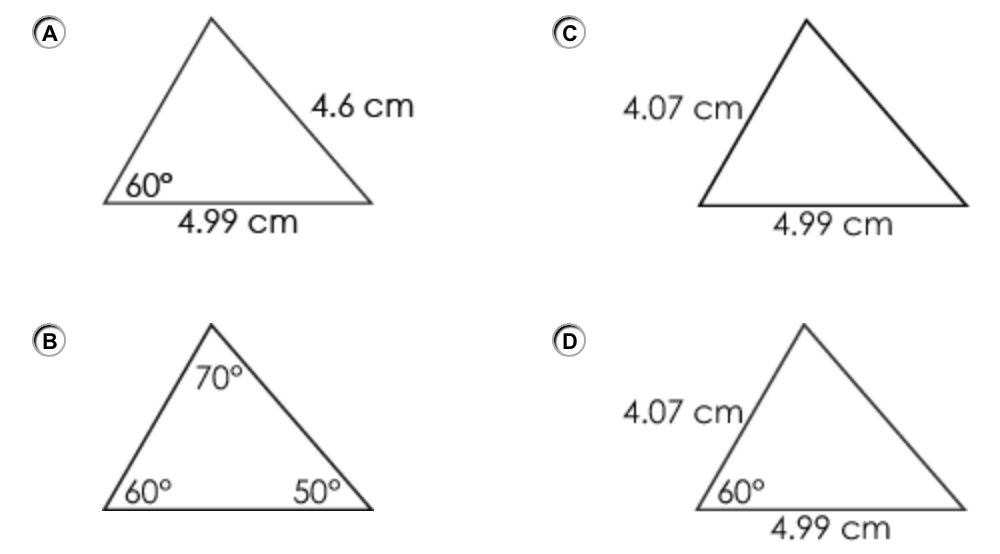
Which triangle can be shown to be congruent to ∆MNO with only the given information?

---

There are 4 ways to prove 2 triangles are congruent:

1.) Side-Side-Side (SSS): if 3 sides of one triangle are equal to 3 sides of another triangle, then the 2 triangles are congruent.

2.) Side-Angle-Side (SAS): if 2 sides and the included angle of one triangle are equal to 2 sides and the included angle of another triangle, then the 2 triangles are congruent.

3.) Angle-Side-Angle (ASA): if 2 angles and the included side of one triangle are equal to 2 angles and the included side of another triangle, then the 2 triangles are congruent.

​4.) Angle-Angle-Side (AAS): if 2 angles and a non-included side of one triangle are equal to 2 angles and a non-included side of another triangle, then the 2 triangles are congruent.


The given triangle is congruent to D.)
because of Side-Angle-Side (SAS) - the 2 sides 4.07 and 4.99 are equal in both triangles, as well as the included angle of 60º being equal in both triangles.

Ask Algebra House