Find the missing side of the triangle

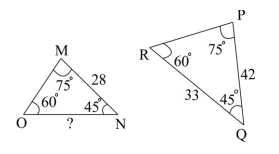
Triangle MNO and triangle PQR are similar.

What is the length in units of segment NO?
A.)  14
B.)  19
C.)  22
D,)  26

---

Since the triangles are similar, set up a proportion to find the length of segment NO.

NO in the left triangle matches up with QR in the right triangle.
MN in the left triangle matches up with PQ in the right triangle.

NO        28
----  =  ----
33          42

42(NO) = 33(28)   {cross-multiplied}
42(NO) = 924   {multiplied 33 by 28}
NO = 22   {divided each side by 42}

C.)  22

Ask Algebra House