Find the Area

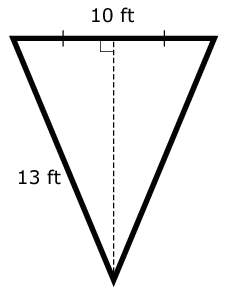
A sign company is building a sign with the dimensions shown.

What is the area, in square feet, of the sign?

---

Since the top of the sign has a length of 10 feet, split into two equal sections, then each section of the top is 5 feet.

The height of the triangle can be found by using the Pythagorean Theorem on either the left or right triangle.

Pythagorean Theorem
a² + b² = c²   {sum of the squares of the legs is equal to the square of the hypotenuse}
5² + b² = 13²   {substituted 5 in for a leg and 13 in for the hypotenuse, into the Pythagorean Theorem}
25 + b² = 169   {evaluated exponents}
b² = 144   {subtracted 25 from each side}
b = 12   {took square root of each side}

height of triangle is 12 ft

base x height
-------------  =  area of a triangle
          2

10 x 12
-------  =  area   {substituted 10 for base and 12 for height, of triangle, into area formula}
    2

120
----  =  area   {multiplied 10 by 12}
  2

area = 60 ft²

Ask Algebra House