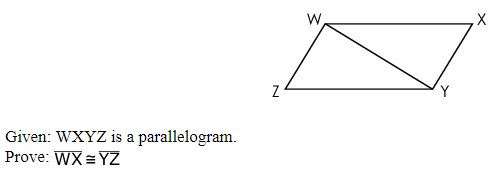Complete the Proof

A parallelogram and an incomplete proof are shown.

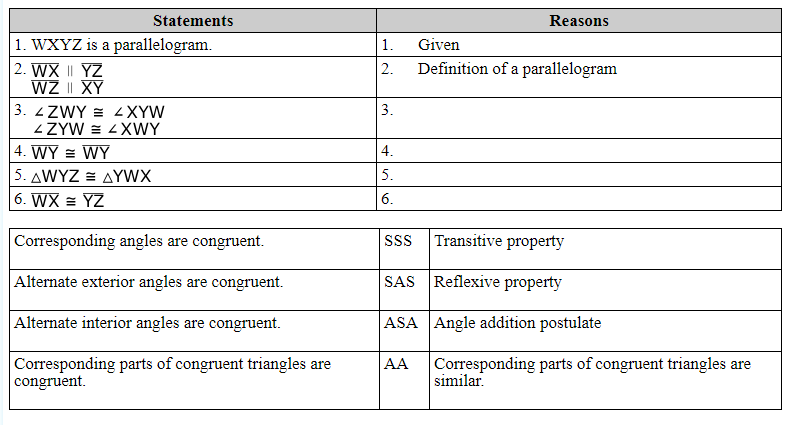
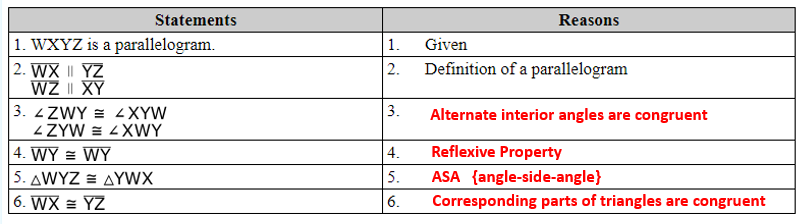
Place reasons in the table to complete the proof:

---

Alternate interior angles are congruent

• If two parallel lines are cut by a transversal, then their pairs of alternate interior angles are congruent
• Alternate interior angles are on alternate sides of the transversal and on the interior of the parallel lines

Reflexive Property

• A value is equal to itself

ASA  (angle-side-angle)

• If two angles and the included side of one triangle are congruent to two angles and the included side of another

            triangle, then the two triangles are congruent

Corresponding parts of congruent triangles are congruent

• That one is just common sense!

Ask Algebra House