Stretch and reflection of a graph

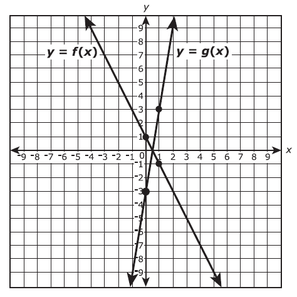
The figure shows the graphs of the functions y = f(x) and y = g(x).  The four indicated points all have integer coefficients.

If g(x) = k∙f(x), what is the value of k?
​

---

This question is comparing the stretch of f(x) to arrive at g(x).
A graph is stretched away from the x-axis by multiplying the y-value by a number greater than 1.
A graph is reflected over the x-axis by taking the negative of the y-value.

These two are combined, in this particular situation, to create a stretch and a reflection.  

Note on f(x), the point (1,-1).
Also note on g(x), the point (1,3).
For an x value of 1, the y-value is multiplied by -3.

Note on f(x), the point (0,1).
Also note on g(x), the point (0,-3).
For an x value of 0, the y-value is multiplied by -3.

Thus, since the y-value in f(x) is being multiplied by -3,
a stretch of 3 and a reflection over the x-axis are created to arrive at g(x).

k = -3

Ask Algebra House
​