Stretch and reflection of a function

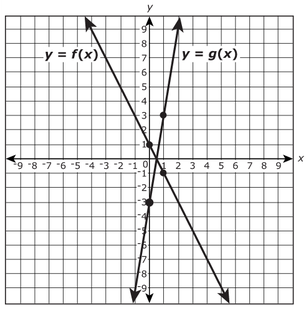
The figure shows the graphs of the functions y = f(x) and y = g(x).  The four indicated points all have integer coefficients.

If g(x) = k(f(x), what is the value of k?

---

Notice on f(x), the indicated points are (0,1) and (1,-1)
Also, on g(x), the indicated points are (0,-3) and (1,3)

The question is, what are you multiplying the y-value on f(x) to get the corresponding y-value on g(x)?

In other words, what do you multiply 1 by to get -3, in  both sets of corresponding points?

k = -3

When multiplying f(x) by -3,
- the negative sign indicates a reflection over the x-axis, as you are taking the negative of the y-value
- the 3 indicates a stretch, away from the x-axis, by a factor of 3, as you are multiplying the y-value by 3

Ask Algebra House