Solving a quadratic equation by factoring

An equation is shown.

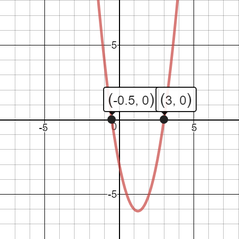
2x² - 5x - 3 = 0

​What value of x makes the equation true?

---

Factor the quadratic expression into two binomials, by grouping.
2x² - 5x - 3 = 0
2x² - 6x + x - 3 = 0   {split -5x, into  two terms whose coefficients multiply to get 2(-3) and add to get -5}
2x(x - 3) + 1(x - 3) = 0   {factored 2x out of first two terms and 1 out of last two terms}
(2x + 1)(x - 3) = 0   {factored (x - 3) out of the two terms}
2x + 1 = 0   or   x - 3 = 0   {set each factor equal to zero}
2x = -1   or   x = 3   {subtracted 1 from each side of first equation and added 3 to each side of second equation}
x = -1/2   or   x = 3   {divided first equation by 2}

The x-intercepts of the parabola formed representing the function f(x) = 2x² - 5x - 3  are  -1/2  and  3.

Ask Algebra House
​