Solving a quadratic equation by factoring

The expression 3x² - 33x - 180 can be factored into the form a(x + b)(x + c), where a, b, and c are constants, to reveal the zeros of the function defined by the expression.  What are the zeros of the function defined by 3x² - 33x - 180?  

Select all that apply.

A.)  -15
B.)  -10
C.)  -6
D.)  -4
E.)  4
F.)  6
G.)  10
H.)  15

---

To find the zeros, set the expression equal to zero and solve for x.

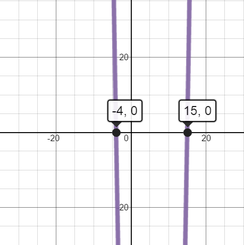
3x² - 33x - 180 = 0    {set the expression equal to zero}
3(x² - 11x - 60) = 0   {factored out the greatest common factor, 3}
3(x - 15)(x + 4) = 0   {factored into two binomials}
(x - 15)(x + 4) = 0   {divided each side by 3}
x - 15 = 0   or   x + 4 = 0   {set each factor equal to 0}
x = 15   or   x = -4   {solved each equation for x}

D.)  -4  and   H.)  15


Zeros are the x-intercepts.  Where the parabola crosses the x-axis, because the value of y is zero in the function f(x) = 3x² - 33x - 180.

Ask Algebra House