Solve a Linear-Quadratic System of Equations

A system of equations is given.

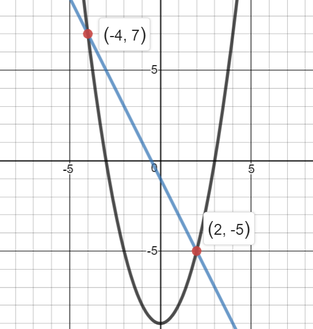
y = x² - 9
y = -2x - 1

What is one solution to the system?

---

A solution to a system of equations is the (x,y) coordinates where the two graphs intersect.

Since both, x² - 9 and -2x - 1 are equal to y, then set them equal to each other and solve for x.

x² - 9 = -2x - 1   
+2x + 1   +2x + 1

x² + 2x - 8 = 0   {added 2x and 1 to each side}
(x + 4)(x - 2) = 0   {factored into two binomials}
x + 4 = 0   or   x - 2 = 0   {set each factor equal to zero}
x = -4   or   x = 2   {solved each equation for x}

Substitute both values for x into one of the two original equations to solve for y.

If x = -4,
y = -2(-4) - 1   {substituted -4, in for x, into second original equation}
y = 8 - 1   {multiplied -2 by -4}
y = 7   {subtracted}
(-4,7) is one solution

If x = 2,
y = -2(2) - 1   {substituted 2, in for x, into second original equation}
y = -4 - 1   {multiplied -2 by 2}
y = -5   {subtracted}
(2,-5) is one solution

(-4,7) and (2,-5) are two solutions to the equation.  They are the points of intersection of the straight line and the
​parabola (as shown below)

​​Ask Algebra House