Quadratic Equation

An equation is shown.

16x² + 10x - 27 = -6x + 5

What are the solutions to the equation?

---

Get all terms to one side of the equation, with zero on the other side of the equal sign.

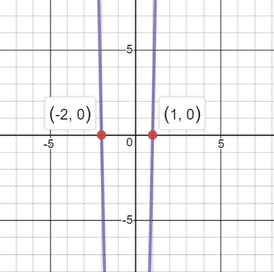
16x² + 10x - 27 = -6x + 5
16x² + 16x - 32 = 0   {added 6x and subtracted 5 from each side}
16(x² + x - 2) = 0   {factored out the common factor of 16}
x² + x - 2 = 0   {divided each side by 16}
(x + 2)(x - 1) = 0   {factored into two binomials...1st terms are x....2nd terms multiplied to get -2 and added to get 1}
x + 2 = 0   or   x - 1 = 0    {since those factors multiplied to equal zero, either one could be zero}
x = -2   or   x = 1   {solved each equation for x}

Ask Algebra House

The graph of a quadratic equation is a parabola.  When you solve a quadratic equation for x, you are finding 
​the x-intercepts (where the graph crosses the x-axis).  There are different ways to solve a quadratic equation, such as, by factoring (as shown above), completing the square, using the quadratic formula, and by using a graphing calculator.