Modeling with a Quadratic Function

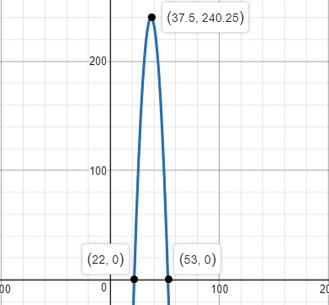
The manager of a company uses the function shown to model its profit based on the price of a product in dollars, x.

f(x) = (x - 2)(53 - x)
​

A.)  What is the minimum price, 
in dollars, to avoid a loss?

B.)  What is the maximum price, 
in dollars, to avoid a loss?

C.)  What is the price, in dollars, that 
results in the greatest profit?

---

If you use the graphing calculator, you will see:

The graph of this quadratic function would be a parabola, with:
- the x-axis representing the price of the product 
- the y-axis representing the total profit

A.)  $22 is the minimum price to avoid a loss    {an x-intercept where the profit is $0}
B.)  $53 is the maximum price to avoid a loss   {an x-intercept where the profit is $0}
C.)  $37.50 is the price that results in the greatest profit   {the maximum/vertex of the parabola}
​
Ask Algebra House
​