|
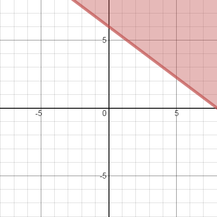
Which is a graph of the solution set of the inequality 3x - 4y ≤ 24?
To graph 3x - 4y ≤ 24: - first graph the boundary line, which is the graph of the equation 3x - 4y = 24, by getting it into slope-intercept form y = mx + b 3x - 4y = 24 -4y = -3x + 24 {subtracted 3x from each side} y = (3/4)x - 6 {divided each side by -4} slope is 3/4 y-intercept is -6 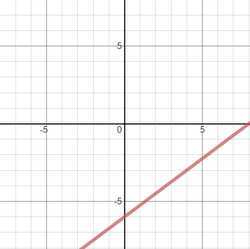
To graph the line y = (3/4)x - 6 - put a point on -6 on the y-axis {the y-intercept} - from there, move up 3 and to the right 4 and put another point {using the slope} - draw a solid line through the two points, since it is a ≤ sign in the original inequality
Change 3x - 4y ≤ 24 to "slope-intercept form" to determine which direction the shading goes. 3x - 4y ≤ 24 -4y ≤ -3x + 24 {subtracted 3x from each side} y ≥ (3/4)x - 6 {divided each side by -4 and changed the inequality sign since dividing by a negative} Since the inequality sign is ≥, within slope-intercept form, then shade above the boundary line. 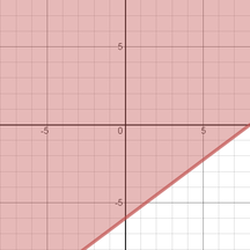
Comments are closed.
|
Latest Videos
Algebra 1 State Test Practice Archives
November 2023
|