Function intervals of increasing or decreasing

Use the information provided to answer Part A and Part B.

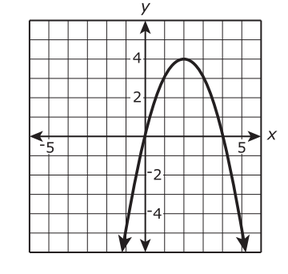
The function f(x) = 4x - x² is graphed in the x-y coordinate plane as shown.

Part A
Based on the graph of the function, which statements are true?  Select all that apply.
A.)  f is increasing on the interval x < 0
B.)  f is decreasing on the interval x < 0
C.)  f is increasing on the interval 0 < x < 2
D.)  f is decreasing on the interval 0 < x < 2
E.)  f is increasing on the interval 2 < x < 4
F.)  f is decreasing on the interval 2 < x < 4
G.)  f is increasing on the interval x > 4
H.)  f is decreasing on the interval x > 4
​

Part B
Based on the graph of the function, which statements are true?  Select all that apply.
A.)  f(x) < 0 on the interval x < 0
B.)  f(x) > 0 on the interval x < 0
C.)  f(x) < 0 on the interval 0 < x < 2
D.)  f(x) > 0 on the interval 0 < x < 2
E.)  f(x) < 0  on the interval 2 < x < 4
F.)  f(x) > 0 on the interval 2 < x < 4
G.)  f(x) < 0 on the interval x > 4
H.)  f(x ) > 0 on the interval x > 4

---

Part A.
Looking at the graph, you can see the function is increasing (rising) as x moves from  - ∞ to  2.

Also, the function is decreasing (falling) as x moves 
from 2 to + ∞.

Therefore, true statements include:
A.)  f is increasing on the interval x < 0
C.)  f is increasing on the interval 0 < x < 2
F.)  f is decreasing on the interval 2 < x < 4
H.) f is decreasing on the interval x > 4
​
Ask Algebra House
​

Part B.
​Looking at the graph, you can see f(x) (the y-value) is greater than zero for x-values between 0 and 4.

Also, f(x) is less than zero when x < 0 and when x > 4.

Therefore, true statements include:
A.)  f(x) < 0 on the interval x < 0
D.)  f(x) > 0 on the interval 0 < x < 2
F.)  f(x) > 0 on the interval 2 < x < 4
G.)  f(x) < 0 on the interval x > 4