Find the solution to the system

A system of equations is given
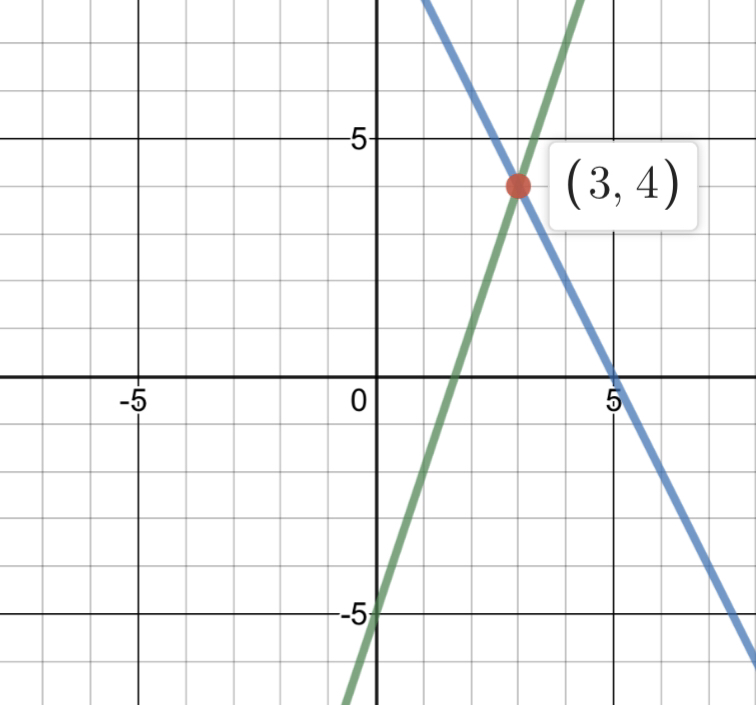
y + 2 = 3(x - 1)
​y = -2x + 10

What is the solution to the system?

---

When finding the solution to a linear system, such as this, you are finding the point of intersection of the two lines.

y + 2 = 3(x - 1)
y = -2x + 10

Substituted (-2x + 10), in for y, into first equation.

-2x + 10 + 2 = 3(x - 1) {substituted (-2x + 10), in for y, into first equation}
-2x + 12 = 3x - 3 {combined like terms and used distributive property}
5x = 15 {added 2x and 3 to each side}
x = 3 {divided each side by 5}

Substitute 3, in for x, into second original equation.

y = -2x + 10 {second original equation}
y = -2(3) + 10 {substituted 3, in for x, into second original equation}
y = -6 + 10 {multiplied -2 by 3}
y = 4 {added}

x = 3 and y = 4

(3,4) is the solution to the system.

Therefore, (3,4) is the point of intersection of the two lines.

Ask Algebra House
​