Solving an absolute value equation {ACT}

If the |x + 1| = 6, what are the possible values for x?
A.) -5 and 7
B.) -1 and 1
C.) 5 and -7 
D.) 5 and -5
E.) 5 and 7

For a more basic example:
If |x| = 3, 
then x could equal 3 or -3, because the absolute value of 3 is 3, and the absolute value of -3 is also 3

|x + 1| = 6
x + 1 = 6    or    x + 1 = -6   {set the value of the expression inside the absolute value symbols equal to 6 and -6}
x = 5   or   x = -7   {subtracted 1 from each side in both equations}

C.)  5 and -7 are the possible values for x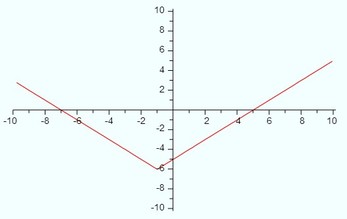

Also if you take the original equation,
|x + 1| = 6, and subtract 6 from each side

|x + 1| - 6 = 0   {subtracted 6 from each side}
then graph the function, f(x) = |x + 1| - 6,  

you can see that when the value of y {or f(x)}
is equal to 0 {also known as the x-intercept}
the value of x is, in fact, equal to -7 and 5, meaning
the graph crosses the x-axis at -7 and 5

---

- Algebra House