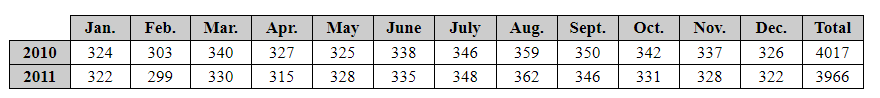|
The two-way table shows the number of births, in thousands, in the United States for the years 2010 and 2011.
A baby born in 2011 is randomly selected.
What is the probability that the baby was born in February? |
Geometry State Test Practice Archives
November 2019
|