Solve the system of non-linear equations

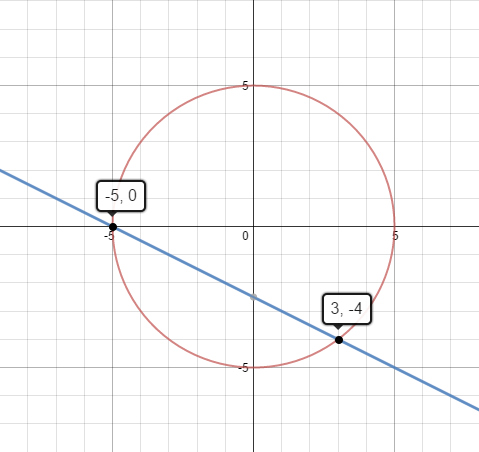
How do you solve this system of non-linear equations?
x² + y² = 25
2x + 4y = -10

When solving the system of those two equations, you are finding the point(s) of intersection of a circle and a straight line.

x² + y² = 25   {a circle}
2x + 4y = -10    {a straight line}

Isolate a variable on the linear equation:
2x + 4y = -10 {the second equation}
2x = -4y - 10 {subtracted 4y from each side}
x = -2y - 5 {divided each side by 2} 

Substitute the value of that variable into the non-linear equation:
x² + y² = 25 {the first equation}
(-2y - 5)² + y² = 25 {substituted (-2y - 5) , in for x, into top equation}
(-2y - 5)(-2y - 5) + y² = 25 {when squaring a binomial, multiply it by itself}
4y² + 20y + 25 + y² = 25 {used foil method}
5y² + 20y + 25 = 25 {combined like terms}
5y² + 20y = 0 {subtracted 25 from each side}
5y(y + 4) = 0 {factored out the common factor, 5y}
5y = 0 or y + 4 = 0 {set each factor equal to 0}
y = 0 or y = -4 {solved each equation} 

x = -2y - 5 {the re-arranged second equation}
If y = 0:
x = -2(0) - 5 {substituted 0 for y}
x = 0 - 5 {multiplied}
x = -5 {subtracted}
(-5,0) is a solution {a point of intersection of the line and circle} 

x = -2y - 5 {the re-arranged second equation}
If y = -4:
x = -2(-4) - 5 {substituted -4 for y}
x = 8 - 5 {multiplied}
x = 3 {subtracted}
(3,-4) is a solution {a point of intersection of the line and circle} 

x = -5 when y = 0 and x = 3 when y = -4
(-5,0) and (3,-4) are the points of intersection of the line and circle

- Algebra House