Vertex form of a quadratic equation

If f(x) = 2x² - 8x + 9, which statement regarding the vertex form of f(x) is true?

A.)  In vertex form, f(x) = 2(x - 2)² + 1 and therefore has a minimum value of 1.
B.)  In vertex form, f(x) = 2(x - 2)² + 1 and therefore has a minimum value of -2.
C.)  In vertex form, f(x) = 2(x - 2)² + 4.5 and therefore has a minimum value of 4.5.
D.)  In vertex form, f(x) = 2(x - 2)² + 4.5 and therefore has a minimum value of -2.

---

Standard form of a quadratic:
f(x) = ax² + bx + c
c is the y-intercept of the parabola

Vertex form of a quadratic is:
f(x) = a(x - h)² + k
(h,k) are the coordinates of the vertex

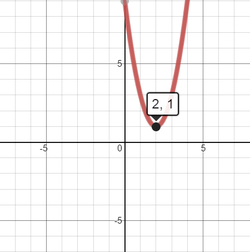
The equation f(x) = 2x² - 8x + 9 is in standard form and must be transformed into vertex form.

To begin, find the x and y coordinates of the vertex, then substitute them along with a which is 2, into vertex form.

The x-coordinate of the vertex is x = -b / 2a

In f(x) = 2x² - 8x + 9
a = 2, b = -8, and c = 9

x = -b/2a   {the x-coordinate of the vertex}
x = -(-8) / 2(2)   {substituted -8 for b and 2 for a into the x-coordinate of the vertex}
x = 8/4   {simplified and multiplied}
x = 2   {divided}

The x-coordinate of the vertex is 2.

To find the y-coordinate of the vertex, substitute 2 in for x into the equation f(x) = 2x² - 8x + 9.

f(x) = 2x² - 8x + 9   {original equation}
f(2) = 2(2)² - 8(2) + 9    {substituted 2 for x}
       = 2(4) - 16 + 9   {evaluated exponent and multiplied}
       = 8 - 16 + 9   {multiplied}
       = 1   {subtracted and added}

The y-coordinate of the vertex is 1.

The vertex has coordinates of (2,1).  In vertex form, these are the coordinates (h,k).

Also the value of a is the same as in standard form, which is 2.

f(x) = a(x - h)² + k   {vertex form of a quadratic equation}
f(x) = 2(x - 2)² + 1   {substituted a,h, and k into vertex form}

In a parabola, which is the graph of a quadratic function, the y-coordinate of the vertex is either the minimum or maximum value.  Since the leading coefficient, 2, is positive, this means the parabola opens upward, and thus has a minimum value.

A.)  In vertex form, f(x) = 2(x - 2)² + 1 and therefore has a minimum value of 1.

Ask Algebra House